Kirchoff's Law

Kirchoff's Law:

Kirchoff's laws allow us to solve complex circuit problems by defining a set of basic network laws and theorems for the voltage and currents around circuit. In 1845, a German physicist, Gustav Kirchoff developed a pair of or set of rules which accomodates conservation of energy and current. These two rules are explained below.

Kirchoff's First Law-The current Law(KCL):

Kirchoff's current law/KCL, states that "the total current or charge entering a junction or node is exactly equal to the leaving the node."
                                                   I(exiting) + I(entering) = 0. 
                                           
                                                    This is conservation of charge.

                                                 

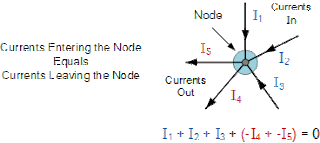
                                                        ∴ I1 + I2 + I3 – I4 – I5 = 0

Kirchoff's Second Law-The Voltage Law(KVL):

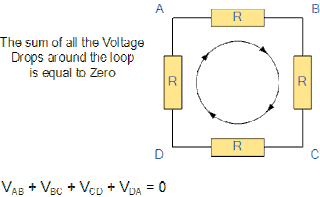
Kirchoff's voltage law /KVL, states that "in any closed loop network, the total voltage around the loop is equal to the sum of all the voltage drops within the same loop." which is also equal to zero.
                                        This is conservation of energy.

   Points to be remembered while going through the loop:

• Starting at any point in the lop continue in the same direction noting the direction of all the voltage drops, either positive or negative and returning to the same starting point.
• It is important to maintain same direction either clockwise or anti-clockwise.
• Suppose we are going through clockwise direction in any loop then if current and our movement direction is same then assign negative sign before taken voltage and vice-versa.
• In case of potential, when we are moving from negative terminal to positive terminal then assign positive sign before that potential.
• Apply kirchoff's current law at each nodes.
• Calculate each current and voltage using Ohm's law and solving simultaneous equations.